Sommaire
On appellera IA un réseau de neurones artificiels
Commençons par définir notre objet d’étude : qu’est-ce qu’une IA ? Par « intelligence artificielle », on pourrait entendre tout dispositif capable de faire réaliser par un ordinateur une opération réputée requérir une tâche cognitive. Dans cette acception, un système expert qui prend des décisions médicales en implémentant les recommandations d’une société savante est une IA. Le pilote automatique d’un avion de ligne est une IA.
Cependant, ce n’est pas la définition la plus couramment employée ces derniers temps. Une IA a battu Lee Sedol au go, mais ça fait des années que des ordinateurs battent les humains aux échecs et personne ne prétend que c’est une IA. Des IA sont employées pour reconnaître des images alors que reconnaître un chien nous semble absolument élémentaire, mais l’algorithme de Youtube qui te suggère des vidéos pouvant te plaire parmi les milliards hébergées fait preuve d’une certaine intelligence et personne ne l’appelle IA. Il semble donc que le terme « IA » s’applique donc à une technique pour effectuer une tâche plus qu’à la tâche en elle-même, ou plutôt à un ensemble de techniques partageant un point commun : le réseau de neurones artificiels.
Dans la suite de cette dépêche, j’utiliserai donc indifféremment les termes d’IA et de réseau de neurones1.
Pour comprendre le réseau de neurones, il est nécessaire de disposer de bases statistiques
Les statistiques (ou la statistique, on peut dire les deux, comme en Alexandrie), c’est la branche des mathématiques qui s’intéresse aux moyens, à partir de données observées et fondamentalement probabilistes, d’en tirer des conclusions généralisables (et idéalement, de prédire l’avenir à partir du passé).
La data science, c’est la branche de l’informatique qui s’intéresse aux moyens, à partir de données emmagasinées sur lesquelles on ne fait pas d’hypothèse de mode de génération, d’en tirer des conclusions généralisables (et idéalement, de prédire les données futures).
Ça vous semble similaire ? Ça l’est. Les deux champs vont avoir des divergences de vocabulaire, de langages (les stateux préfèreront R, les data scientists Python), de formation (les stateux sont plutôt des universitaires, les data scientists plutôt des informaticiens au niveau licence, mais ils ont les mêmes masters et doctorats), mais fondamentalement, et surtout mathématiquement, c’est la même chose. Les connaissances en inférence statistique (notamment bayésienne, pour ceux à qui ça parle) se généralisent très bien à la data science.
Pour faire court, un statisticien est un data scientist qui se la pète, alors qu’un data scientist est un informaticien qui, n’étant pas assez bon pour survivre à la rude concurrence universitaire, a multiplié son salaire par 10 ou 20 en allant vendre ses compétences statistiques à Facebook.
Les statistiques reposent sur la modélisation
En statistique, la manière la plus courante de répondre à une question est de construire un modèle. Prenons une question simple : je dispose d’un jeu de données où j’ai enregistré, pour 1000 personnes, leur IMC et leur taux de cholestérol. Je souhaite savoir s’il y a un lien entre les deux. On souhaiterait, dans ce cas simple, rechercher une relation monotone, sans faire d’hypothèse sur le type de relation.
Un exemple : la régression linéaire
Une manière de répondre à ma question est d’écrire <img style="display: inline; max-height: 1em;" class="mathjax" src="data:image/svg+xml;base64,PHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGlu%0AayIgdmlld0JveD0iMCAtNzEyLjI3NzQ4OTAwMjU0MSAxMTQ0OC40NDQ0NDQ0%0ANDQ0NDUgNzgyLjU1NDk3ODAwNTA4MTgiIHN0eWxlPSJ3aWR0aDogMjYuNjI3%0AZXg7IGhlaWdodDogMS44MDdleDsgdmVydGljYWwtYWxpZ246IC0wLjI0MWV4%0AOyBtYXJnaW46IDFweCAwcHg7IHBvc2l0aW9uOiBzdGF0aWM7IiB4bWxucz0i%0AaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPjxkZWZzIGlkPSJNYXRoSmF4%0AX1NWR19nbHlwaHMiPjxwYXRoIGlkPSJTVElYV0VCTUFJTkktNDMiIHN0cm9r%0AZS13aWR0aD0iMTAiIGQ9Ik02ODkgNjY0bC0zNyAtMjAwbC0xOCAzYy0xMiAx%0AMDcgLTYxIDE2MyAtMTQ5IDE2M2MtNzQgMCAtMTQ0IC0zOCAtMTk5IC05N2Mt%0ANzIgLTc3IC0xMDggLTE5MSAtMTA4IC0zMDFjMCAtMTQwIDY0IC0yMDUgMTc1%0AIC0yMDVjODIgMCAxNDIgMjkgMjI5IDExOWwxOCAtMTVjLTkwIC0xMDYgLTE3%0AMCAtMTQ5IC0yNzMgLTE0OWMtMTUzIDAgLTI2MSA5NiAtMjYxIDI2MWMwIDE0%0AMSA3NyAyNzIgMTg3IDM1MGM2NCA0NiAxNDAgNzMgMjE5IDczIGMzMyAwIDc1%0AIC0yIDExNyAtMTdjMjAgLTcgMzIgLTcgNDEgLTdjMjAgMCAzMCA2IDM4IDIy%0AaDIxWiI+PC9wYXRoPjxwYXRoIGlkPSJTVElYV0VCTUFJTkktNjgiIHN0cm9r%0AZS13aWR0aD0iMTAiIGQ9Ik00NjUgMTE4bDEzIC0xM2MtNjEgLTg3IC05NSAt%0AMTE0IC0xNDYgLTExNGMtMjcgMCAtNDQgMTYgLTQ0IDQyYzAgMTIgNyA0MyAy%0AMCA5Mmw1NSAyMDdjNCAxNiA3IDI5IDcgMzNjMCAxNSAtNSAyNSAtMjggMjVj%0ALTM2IDAgLTEwMCAtNjEgLTE1MiAtMTQwYy00MCAtNjEgLTU2IC05NiAtOTYg%0ALTI1MGgtNzVsMTQ2IDU1NGM4IDMxIDEzIDQ4IDEzIDYyYzAgMTcgLTIzIDI1%0AIC00MSAyNWgtMjd2MTVjNjAgNyA5OSAxNCAxNTcgMjdsNyAtNiBsLTEyMSAt%0ANDQ3YzkwIDE0NiAxNjggMjExIDIzMCAyMTFjNDYgMCA2NSAtMzAgNjUgLTY3%0AYzAgLTI1IC0xOCAtOTkgLTQ4IC0xOTNjLTE3IC01MiAtMzMgLTExNCAtMzMg%0ALTEyNWMwIC0xMCA3IC0xOCAxNiAtMThjMTYgMCAyOCAxMiA4MiA4MFoiPjwv%0AcGF0aD48cGF0aCBpZD0iU1RJWFdFQk1BSU5JLTZGIiBzdHJva2Utd2lkdGg9%0AIjEwIiBkPSJNNDY4IDMwMWMwIC03NiAtNDAgLTE2NCAtMTA2IC0yMjljLTU4%0AIC01OCAtMTIyIC04MyAtMTg4IC04M2MtOTQgMCAtMTQ3IDUyIC0xNDcgMTM5%0AYzAgMTEyIDc1IDIyNyAxODAgMjgzYzM5IDIxIDc5IDMwIDEyMCAzMGM4MSAw%0AIDE0MSAtNTIgMTQxIC0xNDB6TTM4NCAzMjZjMCA2MSAtMjggOTQgLTcxIDk0%0AYy00NCAwIC04OCAtMzEgLTEyOCAtOTFjLTQ2IC03MCAtNzQgLTE0OSAtNzQg%0ALTIyOGMwIC02MCAzMSAtOTEgNzggLTkxIGM0NCAwIDgyIDI5IDEyMSA4M2M0%0ANiA2MyA3NCAxNTcgNzQgMjMzWiI+PC9wYXRoPjxwYXRoIGlkPSJTVElYV0VC%0ATUFJTkktNkMiIHN0cm9rZS13aWR0aD0iMTAiIGQ9Ik0yNzkgNjc4bC0xNTMg%0ALTU4NWMtNSAtMTggLTggLTM1IC04IC00M2MwIC0xMiA3IC0xOCAxNyAtMThj%0AMTUgMCAzOCAxNiA2NyA1N2wyNSAzNWwxNCAtMTBjLTYwIC05NSAtOTcgLTEy%0ANSAtMTUxIC0xMjVjLTMyIDAgLTQ5IDE5IC00OSA1NmMwIDggMSAyMCA0IDMw%0AbDEzNyA1MjRjMyAxMCAzIDE2IDMgMTljMCAxMiAtMTcgMjIgLTQ5IDIyaC0x%0AOHYxNmM1OSA3IDk2IDE0IDE1NSAyN1oiPjwvcGF0aD48cGF0aCBpZD0iU1RJ%0AWFdFQk1BSU5JLTY1IiBzdHJva2Utd2lkdGg9IjEwIiBkPSJNMzU4IDEwOWwx%0AMiAtMTJjLTU3IC03MCAtMTIxIC0xMDggLTIwNCAtMTA4Yy04MSAwIC0xMzUg%0ANTQgLTEzNSAxMzdjMCAxNTUgMTQ5IDMxNSAyOTkgMzE1YzUzIDAgODIgLTI2%0AIDgyIC02OGMwIC04NiAtMTA1IC0xNjQgLTI4NCAtMTg3Yy0xMCAtMjAgLTEw%0AIC00NiAtMTAgLTYxYzAgLTU1IDM3IC05MSA5MyAtOTFjNDQgMCA3NSAxNiAx%0ANDcgNzV6TTE1MiAyNTJsLTE3IC00NGM4NiAyMSAxMjQgMzkgMTYxIDc0YzMx%0AIDMwIDUwIDY2IDUwIDk3IGMwIDI0IC03IDM5IC0zNSAzOWMtNTcgMCAtMTI1%0AIC03NyAtMTU5IC0xNjZaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhXRUJNQUlO%0ASS03MyIgc3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTM2NiA0NDJsLTIwIC0xNDBo%0ALTE2Yy0xMCA4MyAtNDAgMTE2IC04OSAxMTZjLTM1IDAgLTU5IC0yMCAtNTkg%0ALTU3YzAgLTI3IDE1IC01NiA1NCAtMTAyYzUwIC01OCA2OCAtOTcgNjggLTEz%0ANmMwIC04MyAtNjEgLTEzNCAtMTQ0IC0xMzRjLTE3IDAgLTMyIDEgLTU1IDEw%0AYy0xOSA4IC0zMyA5IC00NCA5cy0yMiAtNSAtMjkgLTIxaC0xNmwyMCAxNTlo%0AMTZjMTQgLTk1IDQ4IC0xMzYgMTAwIC0xMzZjNDcgMCA3NiAyOCA3NiA3NyBj%0AMCAzMiAtMTcgNjYgLTU2IDExNWMtNDMgNTQgLTYzIDk5IC02MyAxMzFjMCA2%0ANiA0NyAxMDggMTIxIDEwOGMxNyAwIDMxIC0zIDU2IC0xMGMxOSAtNiAyOCAt%0ANyAzNiAtN2MxNSAwIDIyIDQgMzAgMThoMTRaIj48L3BhdGg+PHBhdGggaWQ9%0AIlNUSVhXRUJNQUlOSS03NCIgc3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTI5NiA0%0AMjhsLTUgLTMyaC04NGwtODcgLTMyOGMtMSAtNCAtMiAtMTEgLTIgLTE0YzAg%0ALTEzIDYgLTE2IDE1IC0xNmMxNiAwIDMyIDE2IDgxIDc5bDEzIC03Yy02MCAt%0AOTIgLTkxIC0xMjEgLTE0MyAtMTIxYy0yNyAwIC00NiAxMiAtNDYgMzdjMCAx%0AMSA4IDQyIDE2IDc0bDc4IDI5NmgtNzVjLTEgMyAtMSA2IC0xIDZjMCAxMSA5%0AIDIwIDMzIDI1YzMyIDcgOTcgNTYgMTMzIDExMGM0IDYgMTAgOSAxNCA5YzYg%0AMCA5IC0zIDkgLTggYzAgMCAwIC01IC0xIC03bC0yOCAtMTAzaDgwWiI+PC9w%0AYXRoPjxwYXRoIGlkPSJTVElYV0VCTEFUSU4tRTkiIHN0cm9rZS13aWR0aD0i%0AMTAiIGQ9Ik0xMTYgNTA3bDE0NyAxNDhjMTggMTggMjcgMjMgNDIgMjNjMjIg%0AMCAzNSAtMTIgMzUgLTMyYzAgLTE2IC05IC0yOSAtMzAgLTQybC0xNTQgLTk3%0AaC00MHpNNDA4IDE2NGwxNiAtN2MtMzkgLTEwOSAtMTA5IC0xNjcgLTIwOSAt%0AMTY3Yy0xMTggMCAtMTkwIDg5IC0xOTAgMjI3YzAgMTQxIDgxIDI0MyAyMDcg%0AMjQzYzYyIDAgMTA3IC0yNCAxMzkgLTY5YzIwIC0yOCAzMCAtNjAgMzQgLTEx%0ANGgtMzA4YzUgLTc2IDEwIC0xMTUgNDYgLTE2MyBjMjggLTM3IDY1IC01NSAx%0AMTEgLTU1YzY3IDAgMTA1IDMxIDE1NCAxMDV6TTk5IDMwOWgyMDRjLTExIDgx%0AIC0zMiAxMTUgLTk4IDExNWMtNTYgMCAtOTUgLTQwIC0xMDYgLTExNVoiPjwv%0AcGF0aD48cGF0aCBpZD0iU1RJWFdFQk1BSU5JLTcyIiBzdHJva2Utd2lkdGg9%0AIjEwIiBkPSJNMTc2IDIyM2wxNiAzNWMxOSA0MiA1MyA5NSA5NCAxMzhjMjYg%0AMjcgNTYgNDUgNzkgNDVjMjggMCA0NyAtMjEgNDcgLTUxcy0xNyAtNTQgLTQ3%0AIC01NGMtMTggMCAtMjYgMTEgLTM1IDI2Yy02IDEwIC05IDE0IC0xNiAxNGMt%0AMTggMCAtNDYgLTMzIC04MiAtOTRjLTQzIC03NCAtNjEgLTExNCAtMTExIC0y%0AODJoLTc2bDgxIDI5MmMxNCA1MiAxNiA2MSAxNiA4MnMtMTggMjYgLTM4IDI2%0AYy04IDAgLTE2IC0xIC0zMSAtM3YxN2wxNTUgMjdsMyAtMiBaIj48L3BhdGg+%0APHBhdGggaWQ9IlNUSVhXRUJNQUlOSS02RiIgc3Ryb2tlLXdpZHRoPSIxMCIg%0AZD0iTTQ2OCAzMDFjMCAtNzYgLTQwIC0xNjQgLTEwNiAtMjI5Yy01OCAtNTgg%0ALTEyMiAtODMgLTE4OCAtODNjLTk0IDAgLTE0NyA1MiAtMTQ3IDEzOWMwIDEx%0AMiA3NSAyMjcgMTgwIDI4M2MzOSAyMSA3OSAzMCAxMjAgMzBjODEgMCAxNDEg%0ALTUyIDE0MSAtMTQwek0zODQgMzI2YzAgNjEgLTI4IDk0IC03MSA5NGMtNDQg%0AMCAtODggLTMxIC0xMjggLTkxYy00NiAtNzAgLTc0IC0xNDkgLTc0IC0yMjhj%0AMCAtNjAgMzEgLTkxIDc4IC05MSBjNDQgMCA4MiAyOSAxMjEgODNjNDYgNjMg%0ANzQgMTU3IDc0IDIzM1oiPjwvcGF0aD48cGF0aCBpZD0iU1RJWFdFQk1BSU5J%0ALTZDIiBzdHJva2Utd2lkdGg9IjEwIiBkPSJNMjc5IDY3OGwtMTUzIC01ODVj%0ALTUgLTE4IC04IC0zNSAtOCAtNDNjMCAtMTIgNyAtMTggMTcgLTE4YzE1IDAg%0AMzggMTYgNjcgNTdsMjUgMzVsMTQgLTEwYy02MCAtOTUgLTk3IC0xMjUgLTE1%0AMSAtMTI1Yy0zMiAwIC00OSAxOSAtNDkgNTZjMCA4IDEgMjAgNCAzMGwxMzcg%0ANTI0YzMgMTAgMyAxNiAzIDE5YzAgMTIgLTE3IDIyIC00OSAyMmgtMTh2MTZj%0ANTkgNyA5NiAxNCAxNTUgMjdaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhXRUJN%0AQUlOLTNEIiBzdHJva2Utd2lkdGg9IjEwIiBkPSJNNjM3IDMyMGgtNTg5djY2%0AaDU4OXYtNjZ6TTYzNyAxMjBoLTU4OXY2Nmg1ODl2LTY2WiI+PC9wYXRoPjxw%0AYXRoIGlkPSJTVElYV0VCTUFJTkktNDEiIHN0cm9rZS13aWR0aD0iMTAiIGQ9%0AIk01NjQgMGgtMjQ1djE2YzYzIDMgNzcgMTkgNzcgNTNjMCA4IC0xIDE3IC0y%0AIDI2bC0yMCAxMzFoLTIyMGwtNTkgLTExMWMtMTQgLTI2IC0yMiAtNTAgLTIy%0AIC02NmMwIC0xOSAxNSAtMzEgNjIgLTMzdi0xNmgtMTg2djE2YzQ2IDkgNTkg%0AMjYgMTM0IDE1NmwyODUgNDk2aDI2bDkyIC01NTNjMTQgLTg0IDI1IC05NSA3%0AOCAtOTl2LTE2ek0zNjkgMjYybC00NSAyNjNsLTE0OSAtMjYzaDE5NFoiPjwv%0AcGF0aD48cGF0aCBpZD0iU1RJWFdFQk1BSU4tRDciIHN0cm9rZS13aWR0aD0i%0AMTAiIGQ9Ik01OTcgMjJsLTQ2IC00N2wtMjMxIDIzMGwtMjMxIC0yMzBsLTQ2%0AIDQ2bDIzMCAyMzFsLTIzMCAyMzFsNDcgNDZsMjMwIC0yMzBsMjMxIDIzMGw0%0ANiAtNDVsLTIzMCAtMjMyWiI+PC9wYXRoPjxwYXRoIGlkPSJTVElYV0VCTUFJ%0ATkktNDkiIHN0cm9rZS13aWR0aD0iMTAiIGQ9Ik0zODQgNjUzdi0xNmMtNTYg%0ALTcgLTY1IC0xNiAtODIgLTc3bC0xMjAgLTQyOWMtOSAtMzIgLTE1IC01NiAt%0AMTUgLTc2YzAgLTI4IDEyIC0zMiA2OSAtMzl2LTE2aC0yNDR2MTZjNTUgMTAg%0ANjkgMTkgODQgNzVsMTIwIDQ0MWM3IDI1IDEzIDQ2IDEzIDYyYzAgMjUgLTE2%0AIDQwIC03MiA0M3YxNmgyNDdaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhXRUJN%0AQUlOSS00RCIgc3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTg3MiA2NTN2LTE2Yy01%0ANyAtOSAtNjcgLTIzIC04MSAtNzRsLTEyMyAtNDQzYy03IC0yNSAtMTQgLTQ2%0AIC0xNCAtNjJjMCAtMjYgMTggLTQwIDgxIC00MmwtMSAtMTZoLTI3MXYxNmM2%0ANSA3IDg1IDI0IDEwMiA4NmwxMjYgNDU5bC0zNzYgLTU2MWgtMTdsLTYyIDU0%0ANmwtMTE4IC00MjhjLTUgLTE4IC05IC00MyAtOSAtNTRjMCAtMjggMTkgLTQ0%0AIDcwIC00OHYtMTZoLTE5N3YxNmM1MiA2IDY4IDIyIDEwMCAxMzRsMTE0IDQw%0AMSBjOCAyNyAxMiA0NCAxMiA1MmMwIDE5IC0yNCAzMSAtNzQgMzR2MTZoMTgx%0AbDU2IC00OTJsMzM1IDQ5MmgxNjZaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhX%0ARUJNQUlOSS00MyIgc3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTY4OSA2NjRsLTM3%0AIC0yMDBsLTE4IDNjLTEyIDEwNyAtNjEgMTYzIC0xNDkgMTYzYy03NCAwIC0x%0ANDQgLTM4IC0xOTkgLTk3Yy03MiAtNzcgLTEwOCAtMTkxIC0xMDggLTMwMWMw%0AIC0xNDAgNjQgLTIwNSAxNzUgLTIwNWM4MiAwIDE0MiAyOSAyMjkgMTE5bDE4%0AIC0xNWMtOTAgLTEwNiAtMTcwIC0xNDkgLTI3MyAtMTQ5Yy0xNTMgMCAtMjYx%0AIDk2IC0yNjEgMjYxYzAgMTQxIDc3IDI3MiAxODcgMzUwYzY0IDQ2IDE0MCA3%0AMyAyMTkgNzMgYzMzIDAgNzUgLTIgMTE3IC0xN2MyMCAtNyAzMiAtNyA0MSAt%0AN2MyMCAwIDMwIDYgMzggMjJoMjFaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhX%0ARUJNQUlOLTJCIiBzdHJva2Utd2lkdGg9IjEwIiBkPSJNNjM2IDIyMGgtMjYx%0Adi0yNjFoLTY2djI2MWgtMjYxdjY2aDI2MXYyNjFoNjZ2LTI2MWgyNjF2LTY2%0AWiI+PC9wYXRoPjxwYXRoIGlkPSJTVElYV0VCTUFJTkktNDIiIHN0cm9rZS13%0AaWR0aD0iMTAiIGQ9Ik0xMzAgNjUzaDI1MGMxMzkgMCAyMDggLTUxIDIwOCAt%0AMTUwYzAgLTU0IC0yOCAtODkgLTY0IC0xMTNjLTMxIC0yMSAtNjggLTMwIC0x%0AMTEgLTM5di0xYzg2IC0yNiAxMjYgLTc5IDEyNiAtMTUwYzAgLTEzNCAtMTEz%0AIC0yMDAgLTI3NSAtMjAwaC0yNzJ2MTZjNTUgOCA2NiAxOCA4MyA4MGwxMjEg%0ANDM2YzcgMjUgMTEgNDkgMTEgNjRjMCAyOSAtMTQgMzYgLTc3IDQxdjE2ek0y%0ANDggMzYzaDM4YzEzMSAwIDIwMSA1MyAyMDEgMTUyIGMwIDc0IC0zNiAxMDgg%0ALTExNyAxMDhjLTM5IDAgLTQ5IDAgLTU5IC0zNnpNMjM4IDMzMWwtMzIgLTEx%0AOWMtMjAgLTc2IC0zNSAtMTI3IC0zNSAtMTQwYzAgLTI4IDI1IC00MiA2NyAt%0ANDJjMTE1IDAgMTkzIDU5IDE5MyAxNzBjMCA2MiAtMjkgMTA2IC02NyAxMTlj%0ALTIwIDcgLTYzIDEyIC0xMjYgMTJaIj48L3BhdGg+PC9kZWZzPjxnIHN0cm9r%0AZT0iYmxhY2siIGZpbGw9ImJsYWNrIiBzdHJva2Utd2lkdGg9IjAiIHRyYW5z%0AZm9ybT0ibWF0cml4KDEgMCAwIC0xIDAgMCkiPjx1c2UgeGxpbms6aHJlZj0i%0AI1NUSVhXRUJNQUlOSS00MyI+PC91c2U+PHVzZSB4bGluazpocmVmPSIjU1RJ%0AWFdFQk1BSU5JLTY4IiB4PSI2OTQiIHk9IjAiPjwvdXNlPjx1c2UgeGxpbms6%0AaHJlZj0iI1NUSVhXRUJNQUlOSS02RiIgeD0iMTE5OSIgeT0iMCI+PC91c2U+%0APHVzZSB4bGluazpocmVmPSIjU1RJWFdFQk1BSU5JLTZDIiB4PSIxNzA0IiB5%0APSIwIj48L3VzZT48dXNlIHhsaW5rOmhyZWY9IiNTVElYV0VCTUFJTkktNjUi%0AIHg9IjE5ODgiIHk9IjAiPjwvdXNlPjx1c2UgeGxpbms6aHJlZj0iI1NUSVhX%0ARUJNQUlOSS03MyIgeD0iMjQzNyIgeT0iMCI+PC91c2U+PHVzZSB4bGluazpo%0AcmVmPSIjU1RJWFdFQk1BSU5JLTc0IiB4PSIyODMxIiB5PSIwIj48L3VzZT48%0AdXNlIHhsaW5rOmhyZWY9IiNTVElYV0VCTEFUSU4tRTkiIHg9IjMxMzIiIHk9%0AIjAiPjwvdXNlPjx1c2UgeGxpbms6aHJlZj0iI1NUSVhXRUJNQUlOSS03MiIg%0AeD0iMzU4MSIgeT0iMCI+PC91c2U+PHVzZSB4bGluazpocmVmPSIjU1RJWFdF%0AQk1BSU5JLTZGIiB4PSIzOTk4IiB5PSIwIj48L3VzZT48dXNlIHhsaW5rOmhy%0AZWY9IiNTVElYV0VCTUFJTkktNkMiIHg9IjQ1MDMiIHk9IjAiPjwvdXNlPjx1%0Ac2UgeGxpbms6aHJlZj0iI1NUSVhXRUJNQUlOLTNEIiB4PSI1MDY0IiB5PSIw%0AIj48L3VzZT48dXNlIHhsaW5rOmhyZWY9IiNTVElYV0VCTUFJTkktNDEiIHg9%0AIjYwMzIiIHk9IjAiPjwvdXNlPjx1c2UgeGxpbms6aHJlZj0iI1NUSVhXRUJN%0AQUlOLUQ3IiB4PSI2ODcwIiB5PSIwIj48L3VzZT48dXNlIHhsaW5rOmhyZWY9%0AIiNTVElYV0VCTUFJTkktNDkiIHg9Ijc3MzgiIHk9IjAiPjwvdXNlPjx1c2Ug%0AeGxpbms6aHJlZj0iI1NUSVhXRUJNQUlOSS00RCIgeD0iODEyNyIgeT0iMCI+%0APC91c2U+PHVzZSB4bGluazpocmVmPSIjU1RJWFdFQk1BSU5JLTQzIiB4PSI5%0AMDA0IiB5PSIwIj48L3VzZT48dXNlIHhsaW5rOmhyZWY9IiNTVElYV0VCTUFJ%0ATi0yQiIgeD0iOTkyMCIgeT0iMCI+PC91c2U+PHVzZSB4bGluazpocmVmPSIj%0AU1RJWFdFQk1BSU5JLTQyIiB4PSIxMDgzMiIgeT0iMCI+PC91c2U+PC9nPjwv%0Ac3ZnPg==%0A" alt="Cholestérol = A\times IMC + B"> et de trouver les meilleurs A et B pour que la droite « colle » le mieux possible au nuage de points. On démontre que la meilleure droite est celle qui minimise un certain critère, la somme des carrés des erreurs. Une fois qu’on a la meilleure droite possible, on peut faire plein de choses avec :
- On peut rétro-prédire le taux de cholestérol des personnes déjà observées et voir de combien la prédiction s’écarte du réel, ce qui fournit une erreur moyenne de prédiction ;
- On peut faire de même en prédisant juste le taux de cholestérol moyen pour tous les individus et comparer les erreurs moyennes de prédiction, ce qui permet de voir de combien le modèle améliore la prédiction (et donc de quantifier la quantité d’info apportée par la donnée IMC sur la variable cholestérol) ;
- On peut étudier le signe de A : si A est négatif, prendre du poids fait baisser le cholestérol : si A est positif, prendre du poids augmente le cholestérol : si A est nul, le poids n’apporte pas d’info sur le cholestérol.
- Par contre, on ne peut rien dire de la causalité. Tout ce qu’on a observé, ce sont des personnes qui, au même moment, avaient un IMC et un taux de cholestérol donnés. Impossible de dire s’ils ont ce cholestérol parce qu’ils ont cet IMC, s’ils ont cet IMC parce qu’ils ont ce cholestérol, ou s’ils ont ce cholestérol et cet IMC parce qu’ils ont une troisième exposition.
- On peut enfin faire effectuer de la prédiction à notre modèle : en lui passant une personne dont on ne connaît que l’IMC, on peut estimer son taux de cholestérol et assortir cette prédiction d’un niveau de certitude (ça demande un peu plus de maths, mais c’est l’idée).
On peut vouloir ajouter une troisième variable, mettons le tabagisme. On écrira alors :
Avec la variable tabac codée à 0 (non fumeur) ou 1 (fumeur). Noter que notre modèle est alors passé en dimension 3 : on ne cherche plus à faire passer la meilleure droite par rapport au nuage de points en 2D, mais à faire passer le meilleur plan par rapport au nuage de points en 3D. Noter aussi qu’on peut facilement inclure des variables qualitatives : il suffit de les coder 0 ou 1. On peut d’ailleurs inclure des variables à n modalités : il suffit de les recoder en n-1 sous-variables en 0-1 (la modalité de référence étant celle pour laquelle toutes les sous-variables sont à 0).
Les <img style="display: inline; max-height: 1em;" class="mathjax" src="data:image/svg+xml;base64,PHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGlu%0AayIgdmlld0JveD0iLTM1IC03MDcuMjc3NDg5MDAyNTQxIDU1NCA5NDEuNTU0%0AOTc4MDA1MDgxOCIgc3R5bGU9IndpZHRoOiAxLjMyNWV4OyBoZWlnaHQ6IDIu%0AMTY5ZXg7IHZlcnRpY2FsLWFsaWduOiAtMC42MDJleDsgbWFyZ2luOiAxcHgg%0AMHB4OyBwb3NpdGlvbjogc3RhdGljOyIgeG1sbnM9Imh0dHA6Ly93d3cudzMu%0Ab3JnLzIwMDAvc3ZnIj48ZGVmcyBpZD0iTWF0aEpheF9TVkdfZ2x5cGhzIj48%0AcGF0aCBpZD0iU1RJWFdFQk1BSU5JLTNCMiIgc3Ryb2tlLXdpZHRoPSIxMCIg%0AZD0iTS05IC0xMjdsMTM3IDQ5NWMzOSAxMzkgMTA4IDMxMCAyNjUgMzEwYzUz%0AIDAgMTIxIC0yNSAxMjEgLTEwMWMwIC04MSAtNjggLTE1NCAtMTI4IC0xODF2%0ALTFjMzggLTMgODggLTQwIDg4IC0xMTFjMCAtOTMgLTg0IC0yMTQgLTE3NyAt%0AMjY1Yy0zOSAtMjIgLTgxIC0zMCAtMTI0IC0zMGMtMjEgMCAtNDAgNSAtNjYg%0AMTdsLTM4IC0xMzNjLTEyIC00MyAtMjIgLTYzIC0zMSAtNzhoLTc4YzkgMTQg%0AMjUgNTcgMzEgNzh6TTIzMyA0NzcgbC0xMTQgLTQzMmMwIC0yMiAyMCAtMzcg%0ANDggLTM3YzExNCAwIDIxOCAxNzUgMjE4IDMwOWMwIDM1IC0xMiA1OSAtNDAg%0ANTljLTE4IDAgLTMzIC04IC01MCAtOGMtMTggMCAtMzAgMTAgLTMwIDIyYzAg%0AMTEgOSAyNCA0NCAyNGM4IDAgMjkgLTYgNDMgLTZjNDMgMCA5MCAxMDAgOTAg%0AMTU4YzAgNzcgLTMyIDkxIC02NyA5MWMtNzMgMCAtMTIwIC05NiAtMTQyIC0x%0AODBaIj48L3BhdGg+PC9kZWZzPjxnIHN0cm9rZT0iYmxhY2siIGZpbGw9ImJs%0AYWNrIiBzdHJva2Utd2lkdGg9IjAiIHRyYW5zZm9ybT0ibWF0cml4KDEgMCAw%0AIC0xIDAgMCkiPjx1c2UgeGxpbms6aHJlZj0iI1NUSVhXRUJNQUlOSS0zQjIi%0APjwvdXNlPjwvZz48L3N2Zz4=%0A" alt="\beta"> sont appelés des paramètres : c’est en les faisant varier qu’on ajuste le modèle aux données.
On peut ainsi ajouter un nombre quelconque de variables… Ou peut-être pas. En effet, on va finir par atteindre un seuil où le meilleur hyperplan est tout simplement celui qui passe par tous les points ! Si j’ai 50 individus et 50 paramètres, il est facile de choisir un plan qui passe par tous les individus. C’est ce qu’on appelle le surapprentissage : le modèle a tout simplement appris le jeu de données par cœur ! Le surapprentissage est un écueil des modèles trop complexes et un réseau de neurones est tout à fait capable de surapprendre.
Le réseau de neurones
Le neurone naturel
Les neurones sont les cellules du système nerveux. Elles sont spécialisées dans la transmission d’information.
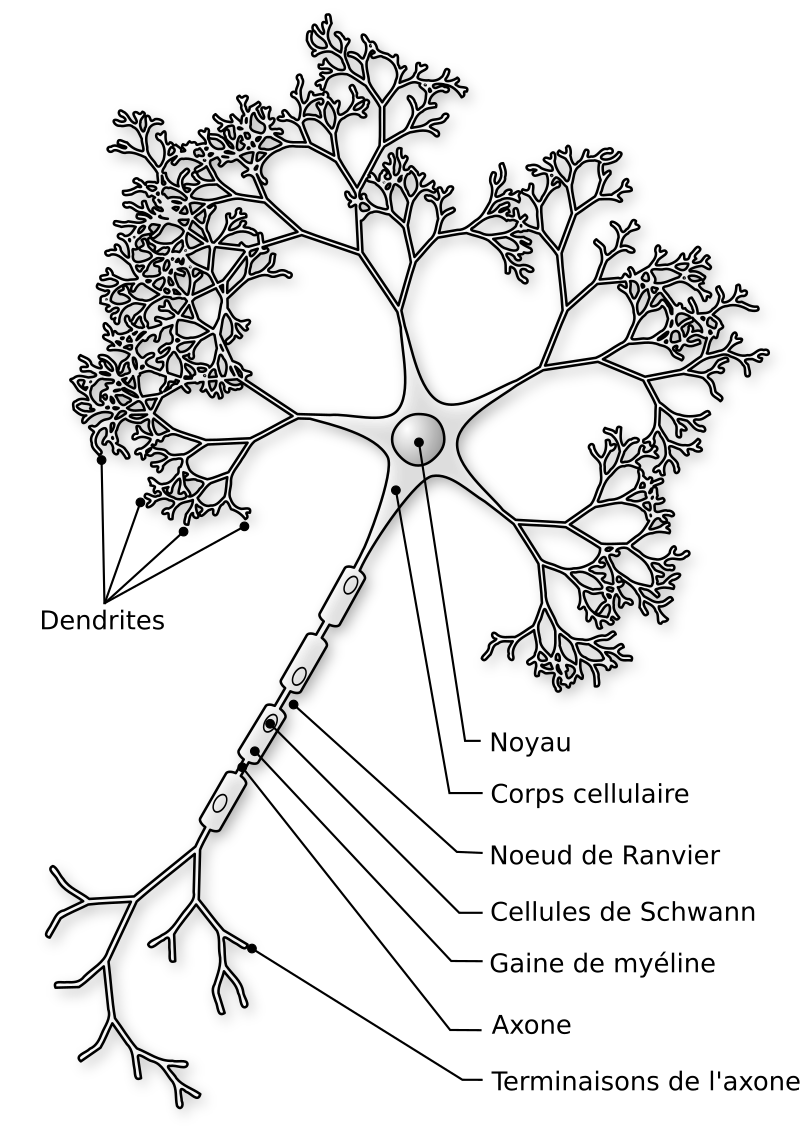
Comme tu peux le voir sur cette image issue de Wikimedia (source), un neurone comprend un nombre quelconque de dendrites, un corps cellulaire, et un axone. Point crucial : l’axone est unique. Il peut lui-même transmettre de l’information à différents neurones en aval, mais il transmet la même information. Or l’information, dans un neurone, peut entrer par les dendrites et par le corps cellulaire, mais elle ne peut ressortir que par l’axone (on peut faire abstraction de la gaine de myéline et des nœuds de Ranvier, qui ont un rôle central dans la vitesse de conduction de l’information mais qui ne changent rien aux calculs effectués). Autrement dit, un neurone transmet la même information à tous les neurones d’aval, et si ceux-ci en font un usage différent, c’est uniquement lié à leurs propres calculs en interne.
Le neurone formel
On peut modéliser un neurone, par analogie avec le neurone naturel. Notre neurone formel pourra donc prendre un nombre quelconque d’entrées, mais comme un neurone naturel, il ne produira qu’une seule sortie. Notre neurone est donc une fonction de ses entrées :
En pratique (mais ça n’a rien d’obligatoire), on prend souvent une fonction d’une combinaison linéaire des entrées :
Avec une contrainte : la fonction <img style="display: inline; max-height: 1em;" class="mathjax" src="data:image/svg+xml;base64,PHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGlu%0AayIgdmlld0JveD0iLTE0MiAtNzA3LjI3NzQ4OTAwMjU0MSA1NzEgOTQzLjU1%0ANDk3ODAwNTA4MTgiIHN0eWxlPSJ3aWR0aDogMS4zMjVleDsgaGVpZ2h0OiAy%0ALjE2OWV4OyB2ZXJ0aWNhbC1hbGlnbjogLTAuNjAyZXg7IG1hcmdpbjogMXB4%0AIDBweDsgcG9zaXRpb246IHN0YXRpYzsiIHhtbG5zPSJodHRwOi8vd3d3Lncz%0ALm9yZy8yMDAwL3N2ZyI+PGRlZnMgaWQ9Ik1hdGhKYXhfU1ZHX2dseXBocyI+%0APHBhdGggaWQ9IlNUSVhXRUJNQUlOSS02NiIgc3Ryb2tlLXdpZHRoPSIxMCIg%0AZD0iTTQxIDQyOGg5M2MyMiA3MSAzOSAxMjYgNzIgMTczYzMwIDQzIDcxIDc3%0AIDEzMiA3N2M0OSAwIDg2IC0yNiA4NiAtNjJjMCAtMjIgLTE5IC00MyAtNDIg%0ALTQzYy0xOCAwIC0zNyAxNSAtMzcgMzljMCAxNyAxMCAyMiAxMCAzMWMwIDgg%0ALTggMTMgLTIyIDEzYy01NiAwIC05MyAtNzAgLTEyMiAtMjI4aDEwN2wtNiAt%0AMzJoLTEwOGwtNzIgLTMyMGMtNDIgLTE4NSAtMTA5IC0yODMgLTIwMCAtMjgz%0AYy00NSAwIC03OSAyNiAtNzkgNjEgYzAgMjMgMTcgNDIgMzggNDJjMjMgMCAz%0AOCAtMTYgMzggLTM3YzAgLTEzIC05IC0xOCAtOSAtMjljMCAtOSA4IC0xNiAy%0AMCAtMTZjNDIgMCA3NCA1NCA5NyAxNjJsODggNDIwaC05MVoiPjwvcGF0aD48%0AL2RlZnM+PGcgc3Ryb2tlPSJibGFjayIgZmlsbD0iYmxhY2siIHN0cm9rZS13%0AaWR0aD0iMCIgdHJhbnNmb3JtPSJtYXRyaXgoMSAwIDAgLTEgMCAwKSI+PHVz%0AZSB4bGluazpocmVmPSIjU1RJWFdFQk1BSU5JLTY2Ij48L3VzZT48L2c+PC9z%0Admc+%0A" alt="f"> (qu’on appelle fonction d’activation) doit être monotone (idéalement strictement monotone), dérivable presque partout (c’est nécessaire à l’optimisation du réseau, qu’on verra plus tard), définie sur un intervalle suffisamment large pour qu’on soit toujours dedans, et non linéaire (sinon mettre les neurones en réseau n’a aucun intérêt, autant faire directement une unique régression linéaire).
En pratique, on prend donc quelques fonctions classiques :
- La fonction binaire :
<img style="display: inline; max-height: 1em;" class="mathjax" src="data:image/svg+xml;base64,PHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGlu%0AayIgdmlld0JveD0iLTE0MiAtNzA3LjI3NzQ4OTAwMjU0MSAzNDQ5LjU1NTU1%0ANTU1NTU1NTcgOTQzLjU1NDk3ODAwNTA4MTgiIHN0eWxlPSJ3aWR0aDogNy45%0ANTJleDsgaGVpZ2h0OiAyLjE2OWV4OyB2ZXJ0aWNhbC1hbGlnbjogLTAuNjAy%0AZXg7IG1hcmdpbjogMXB4IDBweDsgcG9zaXRpb246IHN0YXRpYzsiIHhtbG5z%0APSJodHRwOi8vd3d3LnczLm9yZy8yMDAwL3N2ZyI+PGRlZnMgaWQ9Ik1hdGhK%0AYXhfU1ZHX2dseXBocyI+PHBhdGggaWQ9IlNUSVhXRUJNQUlOSS02NiIgc3Ry%0Ab2tlLXdpZHRoPSIxMCIgZD0iTTQxIDQyOGg5M2MyMiA3MSAzOSAxMjYgNzIg%0AMTczYzMwIDQzIDcxIDc3IDEzMiA3N2M0OSAwIDg2IC0yNiA4NiAtNjJjMCAt%0AMjIgLTE5IC00MyAtNDIgLTQzYy0xOCAwIC0zNyAxNSAtMzcgMzljMCAxNyAx%0AMCAyMiAxMCAzMWMwIDggLTggMTMgLTIyIDEzYy01NiAwIC05MyAtNzAgLTEy%0AMiAtMjI4aDEwN2wtNiAtMzJoLTEwOGwtNzIgLTMyMGMtNDIgLTE4NSAtMTA5%0AIC0yODMgLTIwMCAtMjgzYy00NSAwIC03OSAyNiAtNzkgNjEgYzAgMjMgMTcg%0ANDIgMzggNDJjMjMgMCAzOCAtMTYgMzggLTM3YzAgLTEzIC05IC0xOCAtOSAt%0AMjljMCAtOSA4IC0xNiAyMCAtMTZjNDIgMCA3NCA1NCA5NyAxNjJsODggNDIw%0AaC05MVoiPjwvcGF0aD48cGF0aCBpZD0iU1RJWFdFQk1BSU4tMjgiIHN0cm9r%0AZS13aWR0aD0iMTAiIGQ9Ik0zMDQgLTE2MWwtMTIgLTE2Yy0xNTggOTAgLTI0%0ANCAyNTkgLTI0NCA0MjljMCAxODUgODcgMzI5IDI0NyA0MjRsOSAtMTZjLTEz%0AOSAtMTE5IC0xNzAgLTIxMiAtMTcwIC00MDVjMCAtMTg2IDMwIC0yOTkgMTcw%0AIC00MTZaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhXRUJNQUlOSS03OCIgc3Ry%0Ab2tlLXdpZHRoPSIxMCIgZD0iTTI0MyAzNTVsMTIgLTU3YzcwIDEwNyAxMDcg%0AMTQzIDE1MSAxNDNjMjQgMCA0MSAtMTUgNDEgLTM3YzAgLTIxIC0xNCAtMzYg%0ALTM0IC0zNmMtMTkgMCAtMjggMTcgLTUyIDE3Yy0xOCAwIC01NCAtNDQgLTk4%0AIC0xMjFjMCAtNyAyIC0yMSA4IC00NWwzMiAtMTM0YzcgLTI4IDE2IC00MSAz%0AMCAtNDFjMTMgMCAyNCAxMCA0NyA0MGM5IDEyIDEzIDE4IDIxIDI4bDE1IC05%0AYy01OCAtOTAgLTg0IC0xMTQgLTEyMiAtMTE0IGMtMzIgMCAtNDcgMTggLTU5%0AIDY4bC0yOSAxMTlsLTg4IC0xMTljLTQ0IC01OSAtNjQgLTY4IC05NSAtNjhz%0ALTUwIDE2IC01MCA0MmMwIDIwIDE0IDM2IDM0IDM2YzkgMCAxOSAtNCAzMiAt%0AMTFjMTAgLTYgMjAgLTkgMjYgLTljMTEgMCAzMCAxOSA1MSA0OWw4MiAxMTZs%0ALTI4IDEyNGMtMTQgNjAgLTIxIDY4IC00NiA2OGMtOCAwIC0yMCAtMiAtMzkg%0ALTdsLTE4IC01bC0zIDE2bDExIDRjNjEgMjIgOTQgMjkgMTE3IDI5IGMyNSAw%0AIDM3IC0xOCA1MSAtODZaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhXRUJNQUlO%0ALTI5IiBzdHJva2Utd2lkdGg9IjEwIiBkPSJNMjkgNjYwbDEyIDE2YzE1MyAt%0AOTIgMjQ0IC0yNTkgMjQ0IC00MjljMCAtMTg1IC04OCAtMzI3IC0yNDcgLTQy%0ANGwtOSAxNmMxNDIgMTE3IDE3MCAyMTEgMTcwIDQwNWMwIDE4NyAtMjUgMzAy%0AIC0xNzAgNDE2WiI+PC9wYXRoPjxwYXRoIGlkPSJTVElYV0VCTUFJTi0zRCIg%0Ac3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTYzNyAzMjBoLTU4OXY2Nmg1ODl2LTY2%0Aek02MzcgMTIwaC01ODl2NjZoNTg5di02NloiPjwvcGF0aD48cGF0aCBpZD0i%0AU1RJWFdFQk1BSU4tMzAiIHN0cm9rZS13aWR0aD0iMTAiIGQ9Ik00NzYgMzMw%0AYzAgLTE3MiAtNjMgLTM0NCAtMjI2IC0zNDRjLTE3MSAwIC0yMjYgMTg2IC0y%0AMjYgMzUwYzAgMTc3IDY5IDM0MCAyMzAgMzQwYzEzMSAwIDIyMiAtMTQxIDIy%0AMiAtMzQ2ek0zODAgMzI1YzAgMjA4IC00NCAzMjUgLTEzMiAzMjVjLTgzIDAg%0ALTEyOCAtMTE4IC0xMjggLTMyMXM0NCAtMzE3IDEzMCAtMzE3Yzg1IDAgMTMw%0AIDExNSAxMzAgMzEzWiI+PC9wYXRoPjwvZGVmcz48ZyBzdHJva2U9ImJsYWNr%0AIiBmaWxsPSJibGFjayIgc3Ryb2tlLXdpZHRoPSIwIiB0cmFuc2Zvcm09Im1h%0AdHJpeCgxIDAgMCAtMSAwIDApIj48dXNlIHhsaW5rOmhyZWY9IiNTVElYV0VC%0ATUFJTkktNjYiPjwvdXNlPjx1c2UgeGxpbms6aHJlZj0iI1NUSVhXRUJNQUlO%0ALTI4IiB4PSI0MjkiIHk9IjAiPjwvdXNlPjx1c2UgeGxpbms6aHJlZj0iI1NU%0ASVhXRUJNQUlOSS03OCIgeD0iNzY3IiB5PSIwIj48L3VzZT48dXNlIHhsaW5r%0AOmhyZWY9IiNTVElYV0VCTUFJTi0yOSIgeD0iMTIxOSIgeT0iMCI+PC91c2U+%0APHVzZSB4bGluazpocmVmPSIjU1RJWFdFQk1BSU4tM0QiIHg9IjE4MzQiIHk9%0AIjAiPjwvdXNlPjx1c2UgeGxpbms6aHJlZj0iI1NUSVhXRUJNQUlOLTMwIiB4%0APSIyODAyIiB5PSIwIj48L3VzZT48L2c+PC9zdmc+%0A" alt="f(x) = 0"> si <img style="display: inline; max-height: 1em;" class="mathjax" src="data:image/svg+xml;base64,PHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGlu%0AayIgdmlld0JveD0iLTIyIC03MDUuMjc3NDg5MDAyNTQxIDIyMjQuNTU1NTU1%0ANTU1NTU1NyA3NTguNTU0OTc4MDA1MDgxOCIgc3R5bGU9IndpZHRoOiA1LjE4%0AMWV4OyBoZWlnaHQ6IDEuODA3ZXg7IHZlcnRpY2FsLWFsaWduOiAtMC4yNDFl%0AeDsgbWFyZ2luOiAxcHggMHB4OyBwb3NpdGlvbjogc3RhdGljOyIgeG1sbnM9%0AImh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIj48ZGVmcyBpZD0iTWF0aEph%0AeF9TVkdfZ2x5cGhzIj48cGF0aCBpZD0iU1RJWFdFQk1BSU5JLTc4IiBzdHJv%0Aa2Utd2lkdGg9IjEwIiBkPSJNMjQzIDM1NWwxMiAtNTdjNzAgMTA3IDEwNyAx%0ANDMgMTUxIDE0M2MyNCAwIDQxIC0xNSA0MSAtMzdjMCAtMjEgLTE0IC0zNiAt%0AMzQgLTM2Yy0xOSAwIC0yOCAxNyAtNTIgMTdjLTE4IDAgLTU0IC00NCAtOTgg%0ALTEyMWMwIC03IDIgLTIxIDggLTQ1bDMyIC0xMzRjNyAtMjggMTYgLTQxIDMw%0AIC00MWMxMyAwIDI0IDEwIDQ3IDQwYzkgMTIgMTMgMTggMjEgMjhsMTUgLTlj%0ALTU4IC05MCAtODQgLTExNCAtMTIyIC0xMTQgYy0zMiAwIC00NyAxOCAtNTkg%0ANjhsLTI5IDExOWwtODggLTExOWMtNDQgLTU5IC02NCAtNjggLTk1IC02OHMt%0ANTAgMTYgLTUwIDQyYzAgMjAgMTQgMzYgMzQgMzZjOSAwIDE5IC00IDMyIC0x%0AMWMxMCAtNiAyMCAtOSAyNiAtOWMxMSAwIDMwIDE5IDUxIDQ5bDgyIDExNmwt%0AMjggMTI0Yy0xNCA2MCAtMjEgNjggLTQ2IDY4Yy04IDAgLTIwIC0yIC0zOSAt%0AN2wtMTggLTVsLTMgMTZsMTEgNGM2MSAyMiA5NCAyOSAxMTcgMjkgYzI1IDAg%0AMzcgLTE4IDUxIC04NloiPjwvcGF0aD48cGF0aCBpZD0iU1RJWFdFQk1BSU4t%0AM0MiIHN0cm9rZS13aWR0aD0iMTAiIGQ9Ik02MjEgLTI0bC01NjUgMjczdjEw%0AbDU2NSAyNzV2LTY1bC00MzIgLTIxNWw0MzIgLTIxNXYtNjNaIj48L3BhdGg+%0APHBhdGggaWQ9IlNUSVhXRUJNQUlOLTMwIiBzdHJva2Utd2lkdGg9IjEwIiBk%0APSJNNDc2IDMzMGMwIC0xNzIgLTYzIC0zNDQgLTIyNiAtMzQ0Yy0xNzEgMCAt%0AMjI2IDE4NiAtMjI2IDM1MGMwIDE3NyA2OSAzNDAgMjMwIDM0MGMxMzEgMCAy%0AMjIgLTE0MSAyMjIgLTM0NnpNMzgwIDMyNWMwIDIwOCAtNDQgMzI1IC0xMzIg%0AMzI1Yy04MyAwIC0xMjggLTExOCAtMTI4IC0zMjFzNDQgLTMxNyAxMzAgLTMx%0AN2M4NSAwIDEzMCAxMTUgMTMwIDMxM1oiPjwvcGF0aD48L2RlZnM+PGcgc3Ry%0Ab2tlPSJibGFjayIgZmlsbD0iYmxhY2siIHN0cm9rZS13aWR0aD0iMCIgdHJh%0AbnNmb3JtPSJtYXRyaXgoMSAwIDAgLTEgMCAwKSI+PHVzZSB4bGluazpocmVm%0APSIjU1RJWFdFQk1BSU5JLTc4Ij48L3VzZT48dXNlIHhsaW5rOmhyZWY9IiNT%0AVElYV0VCTUFJTi0zQyIgeD0iNzI5IiB5PSIwIj48L3VzZT48dXNlIHhsaW5r%0AOmhyZWY9IiNTVElYV0VCTUFJTi0zMCIgeD0iMTY5NyIgeT0iMCI+PC91c2U+%0APC9nPjwvc3ZnPg==%0A" alt="x < 0">, <img style="display: inline; max-height: 1em;" class="mathjax" src="data:image/svg+xml;base64,PHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGlu%0AayIgdmlld0JveD0iMCAtNzA1LjI3NzQ4OTAwMjU0MSA1MDUgNzM0LjU1NDk3%0AODAwNTA4MTgiIHN0eWxlPSJ3aWR0aDogMS4yMDVleDsgaGVpZ2h0OiAxLjY4%0AN2V4OyB2ZXJ0aWNhbC1hbGlnbjogLTAuMTJleDsgbWFyZ2luOiAxcHggMHB4%0AOyBwb3NpdGlvbjogc3RhdGljOyIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3Jn%0ALzIwMDAvc3ZnIj48ZGVmcyBpZD0iTWF0aEpheF9TVkdfZ2x5cGhzIj48cGF0%0AaCBpZD0iU1RJWFdFQk1BSU4tMzEiIHN0cm9rZS13aWR0aD0iMTAiIGQ9Ik0z%0AOTQgMGgtMjc2djE1Yzc0IDQgOTUgMjUgOTUgODB2NDQ5YzAgMzQgLTkgNDkg%0ALTMwIDQ5Yy0xMCAwIC0yNyAtNSAtNDUgLTEybC0yNyAtMTB2MTRsMTc5IDkx%0AbDkgLTN2LTU5N2MwIC00MyAyMCAtNjEgOTUgLTYxdi0xNVoiPjwvcGF0aD48%0AL2RlZnM+PGcgc3Ryb2tlPSJibGFjayIgZmlsbD0iYmxhY2siIHN0cm9rZS13%0AaWR0aD0iMCIgdHJhbnNmb3JtPSJtYXRyaXgoMSAwIDAgLTEgMCAwKSI+PHVz%0AZSB4bGluazpocmVmPSIjU1RJWFdFQk1BSU4tMzEiPjwvdXNlPjwvZz48L3N2%0AZz4=%0A" alt="1"> sinon
- La fonction logistique, une amélioration de la fonction binaire :
<img style="display: inline; max-height: 1em;" class="mathjax" src="data:image/svg+xml;base64,PHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGlu%0AayIgdmlld0JveD0iLTE0MiAtOTE4LjY4NzUxMzUyNzY1NTMgNTEwOC43NDk3%0AODE5NDQ4OTQ1IDEzNjYuMzY2NDA1MDgzOTU4OSIgc3R5bGU9IndpZHRoOiAx%0AMS44MDdleDsgaGVpZ2h0OiAzLjEzM2V4OyB2ZXJ0aWNhbC1hbGlnbjogLTEu%0AMDg0ZXg7IG1hcmdpbjogMXB4IDBweDsgcG9zaXRpb246IHN0YXRpYzsiIHht%0AbG5zPSJodHRwOi8vd3d3LnczLm9yZy8yMDAwL3N2ZyI+PGRlZnMgaWQ9Ik1h%0AdGhKYXhfU1ZHX2dseXBocyI+PHBhdGggaWQ9IlNUSVhXRUJNQUlOSS02NiIg%0Ac3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTQxIDQyOGg5M2MyMiA3MSAzOSAxMjYg%0ANzIgMTczYzMwIDQzIDcxIDc3IDEzMiA3N2M0OSAwIDg2IC0yNiA4NiAtNjJj%0AMCAtMjIgLTE5IC00MyAtNDIgLTQzYy0xOCAwIC0zNyAxNSAtMzcgMzljMCAx%0ANyAxMCAyMiAxMCAzMWMwIDggLTggMTMgLTIyIDEzYy01NiAwIC05MyAtNzAg%0ALTEyMiAtMjI4aDEwN2wtNiAtMzJoLTEwOGwtNzIgLTMyMGMtNDIgLTE4NSAt%0AMTA5IC0yODMgLTIwMCAtMjgzYy00NSAwIC03OSAyNiAtNzkgNjEgYzAgMjMg%0AMTcgNDIgMzggNDJjMjMgMCAzOCAtMTYgMzggLTM3YzAgLTEzIC05IC0xOCAt%0AOSAtMjljMCAtOSA4IC0xNiAyMCAtMTZjNDIgMCA3NCA1NCA5NyAxNjJsODgg%0ANDIwaC05MVoiPjwvcGF0aD48cGF0aCBpZD0iU1RJWFdFQk1BSU4tMjgiIHN0%0Acm9rZS13aWR0aD0iMTAiIGQ9Ik0zMDQgLTE2MWwtMTIgLTE2Yy0xNTggOTAg%0ALTI0NCAyNTkgLTI0NCA0MjljMCAxODUgODcgMzI5IDI0NyA0MjRsOSAtMTZj%0ALTEzOSAtMTE5IC0xNzAgLTIxMiAtMTcwIC00MDVjMCAtMTg2IDMwIC0yOTkg%0AMTcwIC00MTZaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhXRUJNQUlOSS03OCIg%0Ac3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTI0MyAzNTVsMTIgLTU3YzcwIDEwNyAx%0AMDcgMTQzIDE1MSAxNDNjMjQgMCA0MSAtMTUgNDEgLTM3YzAgLTIxIC0xNCAt%0AMzYgLTM0IC0zNmMtMTkgMCAtMjggMTcgLTUyIDE3Yy0xOCAwIC01NCAtNDQg%0ALTk4IC0xMjFjMCAtNyAyIC0yMSA4IC00NWwzMiAtMTM0YzcgLTI4IDE2IC00%0AMSAzMCAtNDFjMTMgMCAyNCAxMCA0NyA0MGM5IDEyIDEzIDE4IDIxIDI4bDE1%0AIC05Yy01OCAtOTAgLTg0IC0xMTQgLTEyMiAtMTE0IGMtMzIgMCAtNDcgMTgg%0ALTU5IDY4bC0yOSAxMTlsLTg4IC0xMTljLTQ0IC01OSAtNjQgLTY4IC05NSAt%0ANjhzLTUwIDE2IC01MCA0MmMwIDIwIDE0IDM2IDM0IDM2YzkgMCAxOSAtNCAz%0AMiAtMTFjMTAgLTYgMjAgLTkgMjYgLTljMTEgMCAzMCAxOSA1MSA0OWw4MiAx%0AMTZsLTI4IDEyNGMtMTQgNjAgLTIxIDY4IC00NiA2OGMtOCAwIC0yMCAtMiAt%0AMzkgLTdsLTE4IC01bC0zIDE2bDExIDRjNjEgMjIgOTQgMjkgMTE3IDI5IGMy%0ANSAwIDM3IC0xOCA1MSAtODZaIj48L3BhdGg+PHBhdGggaWQ9IlNUSVhXRUJN%0AQUlOLTI5IiBzdHJva2Utd2lkdGg9IjEwIiBkPSJNMjkgNjYwbDEyIDE2YzE1%0AMyAtOTIgMjQ0IC0yNTkgMjQ0IC00MjljMCAtMTg1IC04OCAtMzI3IC0yNDcg%0ALTQyNGwtOSAxNmMxNDIgMTE3IDE3MCAyMTEgMTcwIDQwNWMwIDE4NyAtMjUg%0AMzAyIC0xNzAgNDE2WiI+PC9wYXRoPjxwYXRoIGlkPSJTVElYV0VCTUFJTi0z%0ARCIgc3Ryb2tlLXdpZHRoPSIxMCIgZD0iTTYzNyAzMjBoLTU4OXY2Nmg1ODl2%0ALTY2ek02MzcgMTIwaC01ODl2NjZoNTg5di02NloiPjwvcGF0aD48cGF0aCBp%0AZD0iU1RJWFdFQk1BSU4tMzEiIHN0cm9rZS13aWR0aD0iMTAiIGQ9Ik0zOTQg%0AMGgtMjc2djE1Yzc0IDQgOTUgMjUgOTUgODB2NDQ5YzAgMzQgLTkgNDkgLTMw%0AIDQ5Yy0xMCAwIC0yNyAtNSAtNDUgLTEybC0yNyAtMTB2MTRsMTc5IDkxbDkg%0ALTN2LTU5N2MwIC00MyAyMCAtNjEgOTUgLTYxdi0xNVoiPjwvcGF0aD48cGF0%0AaCBpZD0iU1RJWFdFQk1BSU4tMzEiIHN0cm9rZS13aWR0aD0iMTAiIGQ9Ik0z%0AOTQgMGgtMjc2djE1Yzc0IDQgOTUgMjUgOTUgODB2NDQ5YzAgMzQgLTkgNDkg%0ALTMwIDQ5Yy0xMCAwIC0yNyAtNSAtNDUgLTEybC0yNyAtMTB2MTRsMTc5IDkx%0AbDkgLTN2LTU5N2MwIC00MyAyMCAtNjEgOTUgLTYxdi0xNVoiPjwvcGF0aD48%0AcGF0aCBpZD0iU1RJWFdFQk1BSU4tMkIiIHN0cm9rZS13aWR0aD0iMTAiIGQ9%0AIk02MzYgMjIwaC0yNjF2LTI2MWgtNjZ2





